The period of a physical pendulum is
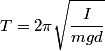 where 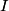 is the moment of inertia about the pivot point and is the moment of inertia about the pivot point and 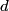 is the distance from the pivot to the center of mass. Let is the distance from the pivot to the center of mass. Let 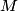 be the mass of hoop be the mass of hoop 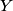 and let and let 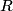 be the radius of hoop be the radius of hoop 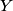 . Then . Then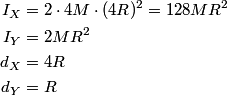 Therefore, 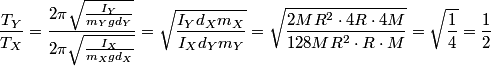 In other words, 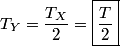 Therefore, answer (B) is correct. |